Игры

Элементарные преобразования матрицы при перестановке. Матричная алгебра - элементарные преобразования матриц

Матрица преобразований применяется для вычисления новых координат объекта при его трансформации. Изменяя значения элементов матрицы преобразования, к объектам можно применять любые трансформации (например: масштабирование, зеркальное отражение, поворот, перемещение и т. п.). При любой трансформации сохраняется параллельность линий объекта.

Координаты в PDF выражаются в терминах двумерного пространства. Точка (x, y) в пространстве может быть выражена в векторной форме . Постоянный третий элемент этого вектора (1) нужен для использования вектора с матрицами 3х3 в вычислениях, описанных ниже.

Преобразование между двумя системами координат представлено, как матрица 3х3 и записывается следующим образом:

Координатные преобразования выражаются в виде матричных умножений:

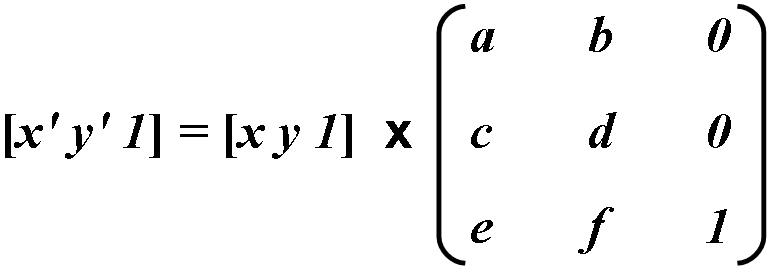
Так как последняя колонка не оказывает ни какого влияния на результаты расчета, то она в вычислениях не принимает участия. Координаты трансформации высчитываются по следующим формулам:

Единичная матрица

Единичной матрицей называется, та у которой значения матрицы a и d равны 1 , а остальные равны 0 . Такая матрица применяется по умолчанию, так как не приводит к трансформации. Поэтому единичную матрицу используют как основу.

Масштабирование

Для увеличения или уменьшения размера объекта по горизонтали/вертикали следует изменить значение a или d соответственно, а остальные применить из единичной матрицы.

Например: Для увеличения размера объекта в два раза по горизонтали, значение a необходимо принять равным 2, а остальные оставить такими как в единичной матрице.

Отражение

Чтобы получить зеркальное отображение объекта по горизонтали следует установить значение a = -1 , по вертикали d = -1 . Изменение обеих значений применяется для одновременного отображения по горизонтали и вертикали.

Наклон

Наклон объекта по вертикали/горизонтали обеспечивается изменением значений b и c соответственно. Изменение значения b/-b - наклон вверх/вниз, c/-c – вправо/влево.

Например: Для наклона объекта по вертикали вверх установим значение b = 1

Высчитываем новые координаты объекта:

В итоге к наклону объекта приводит только координата y , которая увеличивается на значение x .

Поворот

Поворот — это комбинация масштабирования и наклона, но для сохранения начальных пропорций объекта, преобразования должны проводится с точными вычислениями при использовании синусов и косинусов.

Сам поворот происходит против часовой стрелки, α задаёт угол поворота в градусах.

Перемещение

Перемещение осуществляется изменением значений e (по горизонтали) и f (по вертикали). Значения задаются в пикселях.

Например: Перемещение с использованием матрицы применяется редко из-за того, что эту операцию можно проделать другими методами, например, изменить положение объекта во вкладке .

Поскольку матрица трансформации имеет только шесть элементов, которые могут быть изменены, визуально она отображается в PDF . Такая матрица может представлять любое линейное преобразование из одной координатной системы в другую. Матрицы преобразований образуются следующим образом:

Перемещения указываются как , где t x и t y — расстояния от оси системы координат по горизонтали и вертикали, соответственно.
Масштабирование указывается как . Это масштабирует координаты так, что 1 единица в горизонтальном и вертикальном измерениях в новой координатной системе такого же размера, как и s x и s y единиц в старой координатной системе соответственно.
Повороты производятся матрицей , что соответствует повороту осей координатной системы на θ градусов против часовой стрелки.
Наклон указывается как , что соответствует наклону оси x на угол α и оси y на угол β .

На рисунке ниже показаны примеры трансформации. Направления перемещения, угол поворота и наклона, показанные на рисунке, соответствуют положительным значениям элементов матрицы.

Умножения матрицы не коммутативны — порядок, в котором перемножаются матрицы, имеет значение.

В таблице ниже приведены допустимые преобразования и значения матрицы.

Исходный рисунок	Трансформированный рисунок	Матрица	Описание
		1 0 0 2 0 0	Масштаб по вертикали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
		2 0 0 1 0 0	Масштаб по горизонтали. Если значение матрицы больше 1, объект расширяется, меньше 1 — сжимается.
		-1 0 0 1 0 0	Отражение по горизонтали.
		1 0 0 -1 0 0	Отражение по вертикали.
		1 1 0 1 0 0	Наклон по вертикали вверх.
		1 -1 0 1 0 0	Наклон по вертикали вниз.
		1 0 1 1 0 0	Наклон по горизонтали вправо.
		1 0 -1 1 0 0

Элементарные преобразования матрицы находят широкое применение в различных математических задачах. Например, они составляют основу известного метода Гаусса (метода исключения неизвестных) для решения системы линейных уравнений .

К элементарным преобразованиям относятся:

1) перестановка двух строк (столбцов);

2) умножение всех элементов строки (столбца) матрицы на некоторое число, не равное нулю;

3) сложение двух строк (столбцов) матрицы, умноженных на одно и то же число, отличное от нуля.

Две матрицы называются эквивалентными , если одна из них может быть получена из другой после конечного числа элементарных преобразований. В общем случае эквивалентные матрицы равными не являются, но имеют один и тот же ранг.

Вычисление определителей с помощью элементарных преобразований

С помощью элементарных преобразований легко вычислить определитель матрицы. Например, требуется вычислить определитель матрицы:

Тогда можно вынести множитель :

теперь, вычитая из элементов j -го столбца соответствующие элементы первого столбца, умноженные на , получим определитель:

который равен: где

Затем повторяем те же действия для и, если все элементы то тогда окончательно получим:

Если для какого-нибудь промежуточного определителя окажется, что его левый верхний элемент , то необходимо переставить строки или столбцы в так, чтобы новый левый верхний элемент был не равен нулю. Если Δ ≠ 0, то это всегда можно сделать. При этом следует учитывать, что знак определителя меняется в зависимости от того, какой элемент является главным (то есть, когда матрица преобразована так, что ). Тогда знак соответствующего определителя равен .

П р и м е р. С помощью элементарных преобразований привести матрицу

к треугольному виду.

Р е ш е н и е. Сначала умножим первую строку матрицы на 4, а вторую на (–1) и прибавим первую строку ко второй:

Теперь умножим первую строку на 6, а третью на (–1) и прибавим первую строку к третьей:

Наконец, умножим 2-ю строку на 2, а 3-ю на (–9) и прибавим вторую строку к третьей:

В результате получена верхняя треугольная матрица

Пример. Решить систему линейных уравнений, используя матричный аппарат:

Р е ш е н и е. Запишем данную систему линейных уравнений в матричной форме:

Решение данной системы линейных уравнений в матричной форме имеет вид:

где – матрица, обратная к матрице А .

Определитель матрицы коэффициентов А равен:

следовательно, матрица А имеет обратную матрицу .

2. Мальцев А.И. Основы линейной алгебры. – М.: Наука, 1975. – 400 с.

3. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1986. – 544 с.

Матричная алгебра - Элементарные преобразования матриц

Элементарные преобразования матриц

К элементарным преобразованиям относятся:
1) перестановка двух строк (столбцов);
2) умножение всех элементов строки (столбца) матрицы на некоторое число, не равное нулю;
3) сложение двух строк (столбцов) матрицы, умноженных на одно и то же число, отличное от нуля.

Вычисление определителей с помощью элементарных преобразований

где ≠ 0.
Тогда можно вынести множитель :

теперь, вычитая из элементов j - го столбцасоответствующие элементы первого столбца, умноженные на, получим определитель:

который равен: где

Затем повторяем те же действия для и, если все элементы то тогда окончательно получим:

Если для какого-нибудь промежуточного определителя окажется, что его левый верхний элемент , то необходимо переставить строки или столбцы втак, чтобы новый левый верхний элемент был не равен нулю. Если Δ ≠ 0, то это всегда можно сделать. При этом следует учитывать, что знак определителя меняется в зависимости от того, какой элемент является главным (то есть, когда матрица преобразована так, что). Тогда знак соответствующего определителя равен.

П р и м е р. С помощью элементарных преобразований привести матрицу

Следующие три операции называют элементарными преобразованиями строк матрицы :

1) Умножение i-й строки матрицы на число λ ≠ 0:

которое будем записывать в виде (i) → λ(i).

2) Перестановка двух строк в матрице, например i-й и k-й строк:

которую будем записывать в виде (i) ↔ (k).

3) Добавление к i-й строке матрицы ее k-й строки с коэффициентом λ:

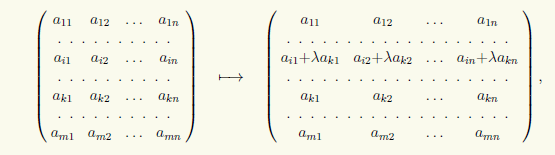
что будем записывать в виде (i) → (i) + λ(k).

Аналогичные операции над столбцами матрицы называют элементарными преобразованиями столбцов .

Каждое элементарное преобразование строк или столбцов матрицы имеет обратное элементарное преобразование , которое преобразованную матрицу превращает в исходную. Например, обратным преобразованием для перестановки двух строк является перестановка тех же строк.

Каждое элементарное преобразование строк (столбцов) матрицы А можно трактовать как умножение A слева (справа) на матрицу специального вида. Эта матрица получается, если то же преобразование выполнить над единичной матрицей . Рассмотрим подробнее элементарные преобразования строк.

Пусть матрица B получается в результате умножения i-й строки матрицы A типа m×n на число λ ≠ 0. Тогда B = Е i (λ)А, где матрица Е i (λ) получается из единичной матрицы E порядка m умножением ее i-й строки на число λ.

Пусть матрица B получается в результате перестановки i-й и k-й строк матрицы А типа m×n. Тогда B = F ik А, где матрица F ik получается из единичной матрицы E порядка m перестановкой ее i-й и k-й строк.

Пусть матрица B получается в результате добавления к i-й строке матрицы А типа m×n ее k-й строки с коэффициентом λ. Тогда B = G ik (λ)А, где матрица G ik получается из единичной матрицы E порядка m в результате добавления к i-й строке k-й строки с коэффициентом λ, т.е. на пересечении i-й строки и k-го столбца матрицы E нулевой элемент заменен на число λ.

Точно так же реализуются элементарные преобразования столбцов матрицы A, но при этом она умножается на матрицы специального вида не слева, а справа.

С помощью алгоритмов, которые основаны на элементарных преобразованиях строк и столбцов, матрицы можно преобразовывать к различному виду. Один из важнейших таких алгоритмов составляет основу доказательства следующей теоремы.

Теорема 10.1. С помощью элементарных преобразований строк любую матрицу можно привести к ступенчатому виду .

◄ Доказательство теоремы состоит в построении конкретного алгоритма приведения матрицы к ступенчатому виду. Этот алгоритм состоит в многократном повторении в определенном порядке трех операций, связанных с некоторым текущим элементом матрицы, который выбирается исходя из расположения в матрице. На первом шаге алгоритма в качестве текущего элемента матрицы выбираем верхний левый, т.е. [A] 11 .

1*. Если текущий элемент равен нулю, переходим к операции 2*. Если же он не равен нулю, то строку, в которой расположен текущий элемент (текущую строку), добавляем с соответствующими коэффициентами к строкам, расположенным ниже, так, чтобы все элементы матрицы, стоящие в столбце под текущим элементом, обратились в нуль. Например, если текущий элемент есть [A] ij , то в качестве коэффициента для k-й строки, k = i + 1, ... , нам следует взять число - [A] kj /[A] ij . Выбираем новый текущий элемент, смещаясь в матрице на один столбец вправо и на одну строку вниз, и переходим к следующему шагу, повторяя операцию 1*. Если такое смещение невозможно, т.е. достигнут последний столбец или строка, преобразования прекращаем.

2*. Если текущий элемент в некоторой строке матрицы равен нулю, то просматриваем элементы матрицы, расположенные в столбце под текущим элементом. Если среди них нет ненулевых, переходим к операции 3*. Пусть в k-й строке под текущим элементом находится ненулевой элемент. Меняем местами текущую и k-ю строки и возвращаемся к операции 1*.

3*. Если текущий элемент и все элементы под ним (в том же столбце) равны нулю, меняем текущий элемент, смещаясь в матрице на один столбец вправо. Если такое смещение возможно, т. е. текущий элемент находится не в самом правом столбце матрицы, то повторяем операцию 1* . Если же мы уже достигли правого края матрицы и смена текущего элемента невозможна, то матрица имеет ступенчатый вид, и мы можем прекратить преобразования.

Так как матрица имеет конечные размеры , а за один шаг алгоритма положение текущего элемента смещается вправо хотя бы на один столбец, процесс преобразований закончится, причем не более чем за n шагов (n - количество столбцов в матрице). Значит, наступит момент, когда матрица будет иметь ступенчатый вид.

Пример 10.10. Преобразуем матрицу к ступенчатому виду с помощью элементарных преобразований строк.