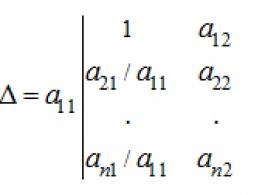Матрицалардың элементар түрлендірулері. Матрицалардың элементар түрлендірулері және олардың қасиеттері Матрицалардың элементар түрлендірулеріне арналған белгілер
Элементар матрицалық түрлендірулерматрицаның осындай түрлендірулері болып табылады, нәтижесінде матрицалардың эквиваленттілігі сақталады. Сонымен, элементар түрлендірулер осы матрица көрсететін сызықтық алгебралық теңдеулер жүйесінің шешімдер жиынын өзгертпейді.
Элементар түрлендірулер матрицаны үшбұрышты немесе сатылы пішінге келтіру үшін Гаусс әдісінде қолданылады.
Анықтама
Элементарлы жол түрлендірулерішақырды:
Кейбір сызықтық алгебра курстарында матрицалық жолдарды ауыстыру жеке элементар түрлендіру ретінде ажыратылмайды, өйткені кез келген екі матрица жолының орнын ауыстыруды кез келген матрица жолын тұрақтыға көбейту арқылы алуға болады. k (\displaystyle k), және матрицаның кез келген жолына тұрақтыға көбейтілген басқа жолды қосу k (\displaystyle k), k ≠ 0 (\displaystyle k\neq 0).
The элементар баған түрлендірулері.
Элементар түрлендірулер қайтымды.
Белгі матрица екенін көрсетеді A (\дисплей стилі A)-дан алуға болады B (\displaystyle B)элементар түрлендірулер арқылы (немесе керісінше).
Қасиеттер
Элементар түрлендірулер кезіндегі инварианттылық дәрежесі
| Теорема (элементар түрлендірулер кезіндегі дәрежелік инварианттық туралы). Егер а A ∼ B (\displaystyle A\sim B), содан кейін r a n g A = r a n g B (\displaystyle \mathrm (қоңырау) A=\mathrm (қоңырау) B). |
Элементар түрлендірулер кезіндегі SLAE эквиваленттілігі
Қоңырау шалайық сызықтық алгебралық теңдеулер жүйесіндегі элементар түрлендірулер :- теңдеулерді ауыстыру;
- теңдеуді нөлдік емес тұрақтыға көбейту;
- бір теңдеуді екінші теңдеуге қосу, кейбір тұрақтыға көбейту.
Кері матрицаларды табу
| Теорема (кері матрицаны табу туралы). Матрицаны анықтауыш болсын A n × n (\displaystyle A_(n\times n))нөлге тең емес, матрица болсын B (\displaystyle B)өрнек арқылы анықталады B = [ A | E ] n × 2 n (\displaystyle B=_(n\times 2n)). Содан кейін, матрица жолдарының элементар түрлендіруі кезінде A (\дисплей стилі A)сәйкестік матрицасына E (\дисплей стилі E)құрамында B (\displaystyle B)түрлендіру бір мезгілде жүреді. E (\дисплей стилі E)дейін A − 1 (\displaystyle A^(-1)). |
Элементар матрицалық түрлендірулер
Элементар матрицалық түрлендірулерәртүрлі математикалық есептерде кеңінен қолданылады. Мысалы, олар сызықтық теңдеулер жүйесін шешуге арналған белгілі Гаусс әдісінің (белгісіздерді жою әдісі) негізін құрайды.
Элементар түрлендірулер:
1) екі жолды (бағандарды) ауыстыру;
2) матрица жолының (бағанының) барлық элементтерін нөлге тең емес қандай да бір санға көбейту;
3) бірдей нөлдік емес санға көбейтілген матрицаның екі жолын (бағандарын) қосу.
Екі матрица деп аталады эквивалент, егер олардың біреуі екіншісінен элементар түрлендірулердің шектеулі санынан кейін алынса. Жалпы алғанда, эквивалентті матрицалар тең емес, бірақ бірдей дәрежеге ие.
Элементар түрлендірулер арқылы анықтауыштарды есептеу
Элементар түрлендірулерді қолдана отырып, матрицалық анықтауышты оңай есептеуге болады. Мысалы, матрицалық анықтауышты есептеу қажет:
мұндағы ≠ 0.
Содан кейін көбейткішті шығаруға болады:

енді элементтерден шегеру j-ші баған, бірінші бағанның сәйкес элементтерін көбейтіп, анықтауышты аламыз:

ол: қайда


Содан кейін біз барлық элементтер үшін бірдей қадамдарды қайталаймыз ![]() содан кейін біз ақырында аламыз:
содан кейін біз ақырында аламыз:

Егер кейбір аралық анықтауыш үшін оның жоғарғы сол элементі болып шықса, онда сол жақ жоғарғы элемент нөлге тең болмайтындай жолдарды немесе бағандарды қайта реттеу керек. Егер ∆ ≠ 0 болса, оны әрқашан жасауға болады. Бұл жағдайда анықтауыштың таңбасы қай элемент негізгі болып табылатынына байланысты өзгеретінін ескеру керек (яғни матрица осылай түрлендіру кезінде). Сонда сәйкес анықтауыштың таңбасы тең болады.
МЫСАЛ Элементар түрлендірулерді пайдаланып, матрицаны келтіріңіз
Элементар матрица ұғымын енгізейік.
АНЫҚТАУ. Жолдар (бағандар) бойынша сингулярлық емес элементар түрлендіру нәтижесінде сәйкестік матрицадан алынған квадрат матрица осы түрлендіруге сәйкес элементар матрица деп аталады.
Мысалы, екінші ретті элементар матрицалар матрицалар болып табылады
мұндағы А – кез келген нөлдік емес скаляр.
Элементар матрица Е сәйкестік матрицасынан келесі сингулярлы емес түрлендірулердің біреуінің нәтижесінде алынады:
1) Е матрицасының жолын (бағанын) нөлдік емес скалярға көбейту;
2) скалярға көбейтілген басқа жолдың (бағанның) Е матрицасының кез келген жолына (бағанына) қосу (немесе азайту).
Жолды нөлге тең емес А скалярға көбейту нәтижесінде Е матрицасынан алынған матрицамен белгілеңіз:

А-ға көбейтілген жолдың жолына қосу (азайту) нәтижесінде Е матрицасынан алынған матрицамен белгілеңіз;

Арқылы жолдар бойынша элементар түрлендіруді қолдану нәтижесінде Е сәйкестік матрицасынан алынған матрицаны белгілейміз; осылайша түрлендіруге сәйкес матрица бар
Элементар матрицалардың кейбір қасиеттерін қарастырыңыз.
МҮЛІК 2.1. Кез келген элементар матрица инверсиялы. Элементар матрицаға кері матрица элементар болып табылады.
Дәлелдеу. Тікелей тексеру кез келген нөлдік емес скаляр А. және еріктілер үшін теңдіктерді көрсетеді.
Осы теңдіктерге сүйене отырып, біз 2.1 қасиетке ие деген қорытындыға келеміз.
МҮЛІК 2.2. Элементар матрицалардың көбейтіндісі инвертивті матрица болып табылады.
Бұл сипат тікелей 2.1 және Қорытынды 2.3 сипаттарынан туындайды.
МҮЛІК 2.3. Егер сингулярлы емес қатардағы элементар түрлендіру - А матрицасын В матрицасына түрлендірсе, онда . Абсурд мәлімдемесі де рас.
Дәлелдеу. Егер жолды нөлдік емес скаляр А-ға көбейту болса, онда

Егер болса, онда

Керісінше де шындық екенін тексеру оңай.
МҮЛІК 2.4. Егер С матрицасы А матрицасынан сингулярлы емес қатардағы элементар түрлендірулер тізбегін пайдаланып алынса, онда . Керісінше де шындық.
Дәлелдеу. 2.3 қасиеті бойынша түрлендіру А матрицасын матрицаға түрлендіреді, матрицаны матрицаға түрлендіреді және т.б. Соңында матрицаны матрицаға түрлендіреді Сондықтан, .
Керісінше де шындық екенін тексеру оңай. Матрицаның инверсиялық шарттары. 2.8 теореманы дәлелдеу үшін келесі үш лемма қажет.
LEMMA 2.4. Нөлдік қатары (бағанасы) бар шаршы матрица инверсия емес.
Дәлелдеу. А нөл жолы бар шаршы матрица, В кез келген матрицасы болсын. А матрицасының нөлдік жолы болсын; содан кейін
яғни AB матрицасының i-ші жолы нөлге тең. Демек, А матрицасы қайтымсыз.
LEMMA 2.5. Егер квадрат матрицаның жолдары сызықты тәуелді болса, онда матрица инвертивті емес.
Дәлелдеу. А сызықты тәуелді жолдары бар шаршы матрица болсын. Содан кейін А-ны қадамдық матрицаға айналдыратын сингулярлы емес қатарлы элементар түрлендірулер тізбегі бар; осындай тізбек болсын. Элементар матрицалардың 2.4 қасиеті бойынша бізде бар
мұндағы С – нөлдік қатары бар матрица.
Демек, Лемма 2.4 бойынша С матрицасы инверсия емес. Екінші жағынан, егер А матрицасы инверсиялы болса, онда (1) теңдіктегі сол жақтағы көбейтінді инверсияланбайтын матрица болар еді, өйткені инверсияланбайтын матрицалардың көбейтіндісі (2.3 қорытындыны қараңыз), бұл мүмкін емес. Демек, А матрицасы қайтымсыз.
Элементар матрицалық түрлендірулерматрицаның осындай түрлендірулері болып табылады, нәтижесінде матрицалардың эквиваленттілігі сақталады. Сонымен, элементар түрлендірулер осы матрица көрсететін сызықтық алгебралық теңдеулер жүйесінің шешімдер жиынын өзгертпейді.
Элементар түрлендірулер матрицаны үшбұрышты немесе сатылы пішінге келтіру үшін Гаусс әдісінде қолданылады.
Анықтама
Элементарлы жол түрлендірулерішақырды:
Кейбір сызықтық алгебра курстарында матрицалық жолдарды ауыстыру жеке элементар түрлендіру ретінде ажыратылмайды, өйткені кез келген екі матрица жолының орнын ауыстыруды кез келген матрица жолын тұрақтыға көбейту және кез келген матрица жолына басқасын қосу арқылы алуға болады. қатары тұрақтыға көбейтінді , .
The элементар баған түрлендірулері.
Элементар түрлендірулер қайтымды.
Белгілеу матрицаны элементар түрлендірулер арқылы алуға болатынын көрсетеді (немесе керісінше).
Қасиеттер
Элементар түрлендірулер кезіндегі инварианттылық дәрежесі
Элементар түрлендірулер кезіндегі SLAE эквиваленттілігі
Қоңырау шалайық сызықтық алгебралық теңдеулер жүйесіндегі элементар түрлендірулер :- теңдеулерді ауыстыру;
- теңдеуді нөлдік емес тұрақтыға көбейту;
- бір теңдеуді екінші теңдеуге қосу, кейбір тұрақтыға көбейту.
Кері матрицаларды табу
| Теорема (кері матрицаны табу туралы). Матрицаның анықтауышы нөл емес болсын, матрица өрнегі арқылы анықталсын. Содан кейін, композициядағы сәйкестік матрицаға матрица жолдарының элементар түрлендіруімен, түрлендіру бір уақытта орын алады. |
Матрицаларды сатылы формаға келтіру
Қадамдық матрицалар түсінігін енгізейік: Матрица бар сатылы көрініс егер: онда келесі мәлімдеме дұрыс болады:Қатысты анықтамалар
Элементар матрица.А матрицасы элементар болып табылады, егер оған ерікті В матрицасын көбейту В матрицасында элементар жолды түрлендіруге әкелетін болса.
Әдебиет
Ильин В.А., Позняк Е.Г. Сызықтық алгебра: Жоғары мектептерге арналған оқулық. - 6-шы басылым, өшірілген. - М .: ФИЗМАТЛИТ, 2004. - 280 б.
Викимедиа қоры. 2010 ж.
Басқа сөздіктерде «Элементарлық матрицалық түрлендірулер» деген не екенін қараңыз:
Кіріспе. Бұл терминнің дәл мағынасында E. бөліктері бастапқы, одан әрі бөлінбейтін бөліктер болып табылады, олардан болжам бойынша барлық материя тұрады. Қазіргі уақытта физика термині «Е. h.» әдетте нақты мағынасында емес, бірақ аты үшін азырақ қолданылады ... ... Физикалық энциклопедия
Кіріспе. E. бөлшектер бұл терминнің дәл мағынасында бастапқы, одан әрі ыдырамайтын бөлшектер, олардан болжам бойынша барлық заттар тұрады. «Е. h.» Қазіргі физикада қарабайыр тұлғалар идеясы өз көрінісін табады, ... ... Ұлы Совет энциклопедиясы
Бұл терминнің басқа да мағыналары бар, Матрица дегенді қараңыз. Матрица — сақина немесе өріс элементтерінің тікбұрышты кестесі ретінде жазылған математикалық объект (мысалы, бүтін, нақты немесе күрделі сандар), ол ... ... Википедияны көрсетеді.
Матрица - бұл сандардың (немесе сақиналы элементтердің) тікбұрышты кестесі ретінде жазылған және онымен басқа ұқсас объектілер арасында алгебралық операцияларды (қосу, алу, көбейту және т.б.) жасауға мүмкіндік беретін математикалық нысан. Орындау ережелері ... ... Уикипедия
Матрица - бұл сандардың (немесе сақиналы элементтердің) тікбұрышты кестесі ретінде жазылған және онымен басқа ұқсас объектілер арасында алгебралық операцияларды (қосу, алу, көбейту және т.б.) жасауға мүмкіндік беретін математикалық нысан. Орындау ережелері ... ... Уикипедия
Матрица - бұл сандардың (немесе сақиналы элементтердің) тікбұрышты кестесі ретінде жазылған және онымен басқа ұқсас объектілер арасында алгебралық операцияларды (қосу, алу, көбейту және т.б.) жасауға мүмкіндік беретін математикалық нысан. Орындау ережелері ... ... Уикипедия
Матрица - бұл сандардың (немесе сақиналы элементтердің) тікбұрышты кестесі ретінде жазылған және онымен басқа ұқсас объектілер арасында алгебралық операцияларды (қосу, алу, көбейту және т.б.) жасауға мүмкіндік беретін математикалық нысан. Орындау ережелері ... ... Уикипедия
Матрица - бұл сандардың (немесе сақиналы элементтердің) тікбұрышты кестесі ретінде жазылған және онымен басқа ұқсас объектілер арасында алгебралық операцияларды (қосу, алу, көбейту және т.б.) жасауға мүмкіндік беретін математикалық нысан. Орындау ережелері ... ... Уикипедия
Анықтама 5.8. Матрицалық жолдардың элементар түрлендірулерікелесі түрлендірулер деп аталады:
1) матрицалық жолды нөлдік емес нақты санға көбейту;
2) матрицаның бір жолына оның басқа жолын ерікті нақты санға көбейту.
Лемма 5.1.Матрицалық жолдардың элементар түрлендірулерінің көмегімен кез келген екі жолды ауыстыруға болады.
Дәлелдеу.
A=  .
. 

 .
.
қадамдық матрица. Матрицалық дәреже
Анықтама 5.9. қадам бастыКелесі қасиеттерге ие матрицаны шақырамыз:
1) егер мен--ші жол нөлге тең болса, онда ( мен+ 1)-ші жол да нөл,
2) егер бірінші нөлдік емес элементтер болса мен-ші және ( мен+ 1)-ші жолдар сандары бар бағандарға орналастырылады кжәне Р, сәйкесінше, содан кейін к < Р.
2-шарт) -дан өту кезінде сол жақтағы нөлдерді міндетті түрде арттыруды талап етеді мен- ші жолға дейін ( мен+ 1)-ші жол. Мысалы, матрицалар
БІРАҚ 1 =  , БІРАҚ 2 =
, БІРАҚ 2 =  , БІРАҚ 3 =
, БІРАҚ 3 =
сатылы және матрицалар
AT 1 =  , AT 2 =
, AT 2 =  , AT 3 =
, AT 3 = 
баспайды.
5.1 теорема.Кез келген матрицаны қарапайым жолды түрлендірулер арқылы қадамдық матрицаға келтіруге болады.
Бұл теореманы мысалмен түсіндірейік.
БІРАҚ= 




 .
.
Алынған матрица қадамдық матрица болып табылады.
Анықтама 5.10. Матрицалық дәрежебіз осы матрицаның сатылы түріндегі нөлдік емес жолдар санын атаймыз.
Мысалы, алдыңғы мысалдағы А матрицасының дәрежесі 3-ке тең.
Өзін-өзі бақылауға арналған сұрақтар
1. Матрица деп нені айтады?
2. Матрицаларды қосу және азайту тәсілдері; матрицаны санға көбейту керек пе?
3. Матрицаны көбейтуге анықтама беріңіз.
4. Қандай матрица транспозицияланған деп аталады?
5. Матрицалық жолдардың қандай түрлендірулері элементар деп аталады?
6. Қадамдық матрицаны анықтаңыз.
7. Матрицаның рангі қалай аталады?
Детерминанттар
Детерминанттарды есептеу
Екінші ретті анықтауыштар
Екінші ретті шаршы матрицаны қарастырайық
Анықтама 6.1. екінші ретті анықтауыш,А матрицасына сәйкес формула бойынша есептелетін сан
│БІРАҚ│= = .
Элементтер а ij деп аталады анықтаушы элементтер│А│, элементтер а 11 , а 22 нысаны негізгі диагональ, және элементтері а 12 , а 21 – жағы.
Мысал. = –28 + 6 = –22.
Үшінші ретті анықтауыштар
Үшінші ретті шаршы матрицаны қарастырайық
БІРАҚ =  .
.
Анықтама 6.2. үшінші ретті анықтауыш,матрицаға сәйкес келеді БІРАҚ, формула бойынша есептелетін сан
│БІРАҚ│= = .
Теңдіктің оң жағындағы қандай өнімдерді қосу белгісімен, ал қайсысы минус белгісімен алынуы керек екенін есте сақтау үшін аталған ережені есте сақтау пайдалы. үшбұрыш ережесі:

Мысал.
1)  = –4 + 0 + 4 – 0 + 2 + 6 = 8.
= –4 + 0 + 4 – 0 + 2 + 6 = 8.
2) = 1, яғни │ Е 3 │= 1.
Үшінші ретті анықтауышты есептеудің басқа әдісін қарастырыңыз.
Анықтама 6.3. Кәмелетке толмаған М ijэлемент a ij анықтауыш - жою арқылы берілгеннен алынған анықтауыш мен-ші жол және j-ші баған. Алгебралық қосуA ijанықтауыштың a ij элементі оның миноры деп аталады M ij, (–1) белгісімен алынған i + j.
Мысал.Кәмелетке толмағанды есептеңіз М 23 және алгебралық қосу БІРАҚ 23 элемент аматрицадағы 23
Кәмелетке толмағанды есептеңіз М 23:
М 23 =  = = –6 + 4 = –2.
= = –6 + 4 = –2.
Содан кейін БІРАҚ 23 = (–1) 2+3 М 23 = 2.
Теорема 6.1.Үшінші ретті анықтауыш кез келген жолдың (бағанның) элементтерінің және олардың алгебралық толықтауыштарының көбейтінділерінің қосындысына тең.
Дәлелдеу.А- приорит
 = . (6.1)
= . (6.1)
Мысалы, екінші қатарды таңдап, алгебралық толықтауыштарды табайық БІРАҚ 21 , БІРАҚ 22 , БІРАҚ 23:
БІРАҚ 21 = (–1) 2+1 = –(![]() ) =
) = ![]() ,
,
БІРАҚ 22 = (–1) 2+2 = ![]() ,
,
БІРАҚ 23 = (–1) 2+3 = –(![]() ) =
) = ![]() .
.
Енді (6.1) формуласын түрлендіреміз.
│БІРАҚ│= (![]() ) + (
) + (![]() ) + (
) + (![]() ) =
) =
= БІРАҚ 21 + БІРАҚ 22 + БІРАҚ 23.
Формула БІРАҚ│= БІРАҚ 21 + БІРАҚ 22 + БІРАҚ 23. шақырды анықтауыштың ыдырауы│БІРАҚ│ екінші жолдың элементтерінің үстінен. Сол сияқты, кеңейтуді басқа жолдардың және кез келген бағанның элементтері бойынша алуға болады
Мысал.
= (екінші бағанның элементтері бойынша) = 1 × (–1) 1+2 + 2 × (–1) 2+2 +
+ (–1)(–1) 3+2 = –(0 + 15) + 2(–2 +20) + (–6 +0) = –15 +36 – 6 = 15.
6.1.3 n-ші ретті анықтауыштар ( n Н)
Анықтама 6.4. анықтауыш nші тапсырыс,матрицаға сәйкес келеді n- ші бұйрық
A = 
кез келген жолдың (бағанның) элементтерінің және олардың алгебралық толықтауыштарының көбейтінділерінің қосындысына тең сан деп аталады, яғни.
│А│= БІРАҚ i1 + А i2 + … + А= ішінде БІРАҚ 1j + А 2j + … + А nj .
Оны қашан байқау қиын емес n= 2 екінші ретті анықтауышты есептеу формуласын аламыз. Егер а n= 1, онда анықтамасы бойынша | деп қабылдаймыз А| = |а | = а .
Мысал.  = (4-ші қатардың элементтері бойынша) = 3×(–1) 4+2 +
= (4-ші қатардың элементтері бойынша) = 3×(–1) 4+2 +
2×(–1) 4+4 = 3(–6 + 20 –2 –32) +2(– 6 +16 +60 +2) = 3(–20) +2×72 = –60 +144 = 84 .
Егер анықтауышта біреуден басқа кез келген жолдың (бағанның) барлық элементтері нөлге тең болса, онда анықтауышты есептеу кезінде оны осы жолдың (бағанның) элементтеріне кеңейту ыңғайлы екенін ескеріңіз.
Мысал.
│Е н│= = 1 × │ E n - 1 │ = … = │Е 3 │= 1.
Анықтауыштардың қасиеті
Анықтама 6.5.матрицаны қарау
 немесе
немесе 
шақырамыз үшбұрышты матрица.
Мүлік 6.1.Үшбұрышты матрицаның анықтаушысы негізгі диагональ элементтерінің көбейтіндісіне тең, яғни.
 =
=  =
= ![]() .
.
Мүлік 6.2.Нөл жолы немесе нөл бағанасы бар матрицаның анықтаушысы нөлге тең.
Мүлік 6.3.Матрицаны ауыстыру кезінде анықтауыш өзгермейді, яғни.
│БІРАҚ│= │А т│.
Мүлік 6.4.Егер матрица ATматрицадан алынады БІРАҚкейбір жолдың әрбір элементін санға көбейту к, содан кейін
│AT│= к│БІРАҚ│.
Мүлік 6.5.
 =
=  +
+  .
.
Мүлік 6.6.Егер матрица ATматрицадан алынады БІРАҚекі жолды ауыстыру, содан кейін AT│= −│БІРАҚ│.
Мүлік 6.7.Пропорционал жолдары бар матрицаның анықтауышы нөлге тең, атап айтқанда, екі бірдей жолы бар матрицаның анықтаушысы нөлге тең.
Мүлік 6.8.Матрицаның анықтаушысы өзгермейді, егер бір жолдың элементтері матрицаның басқа жолының элементтеріне қосылса, қандай да бір санға көбейтіледі.
Пікір. 6.1. 6.3 қасиеті бойынша матрицаның анықтауышы транспозиция кезінде өзгермейтіндіктен, матрицаның жолдары туралы барлық қасиеттер бағандар үшін де дұрыс болады.
Мүлік 6.9.Егер а БІРАҚжәне ATретті квадрат матрицалар болып табылады n, содан кейін │ AB│=│БІРАҚ││AT│.
кері матрица
Анықтама 6.6.шаршы матрица БІРАҚтапсырыс nшақырды қайтымдыматрица болса ATсолай AB \u003d BA \u003d E n. Бұл жағдайда матрица ATшақырды кері матрицаБІРАҚжәне белгіленеді БІРАҚ –1 .
Теорема 6.2.Келесі мәлімдемелер дұрыс:
1) егер матрица БІРАҚинверсиялы болса, онда оған бір кері матрица бар;
2) инверсияланбайтын матрицаның нөлдік емес анықтауышы бар;
3) егер БІРАҚжәне В – ретті инверсиялық матрицалар n, содан кейін матрица ABқайтымды және ( AB) –1 = AT–1× БІРАҚ –1 .
Дәлелдеу.
1. рұқсат етіңіз ATжәне біргематрицаға кері матрицалар болып табылады БІРАҚ, яғни. AB \u003d BA \u003d E nжәне AC \u003d CA \u003d E n. Содан кейін B = BE n = B(AC) = (В.А)C \u003d E n C \u003d C.
2. Матрица болсын БІРАҚқайтымды. Сонда матрица болады БІРАҚ–1 , оның кері, және
А.А –1 = Е н.
Анықтауыштың 6.9 қасиеті бойынша │ А.А –1 │=│БІРАҚ││А –1 │. Содан кейін │ БІРАҚ││БІРАҚ –1 │=│Е н│, қайдан │ БІРАҚ││БІРАҚ–1 │= 1. Демек, │ БІРАҚ│¹ 0.
3. Шынында да,
(AB)(AT –1 БІРАҚ –1) = (БІРАҚ(BB –1))БІРАҚ –1 = (AE n)БІРАҚ –1 = А.А –1 = Е н .
(AT –1 БІРАҚ –1)(AB) = (AT –1 (БІРАҚ-1 A 21 \u003d -1, БІРАҚ 22 = 2. Содан кейін БІРАҚ –1 = .
Өзін-өзі бақылауға арналған сұрақтар
1. Анықтауыш не деп аталады?
2. Оның негізгі қасиеттері қандай?
3. Минор және алгебралық толықтауыш деп нені атайды?
4. Анықтауыштарды есептеудің қандай тәсілдері бар (екінші, үшінші және nтапсырыстар)?
5. Қандай матрица квадрат деп аталады?
Ұқсас ақпарат.